Malthus v/s Romer: ideas, no-rivalidad y la posibilidad de progreso
- Pablo Prieto
- 20 may 2023
- 22 Min. de lectura
Actualizado: 21 may 2023
“Estoy convencido de que tanto los mercados como el libre comercio son buenos, pero la respuesta tradicional que damos a los estudiantes para explicar por qué son buenos—aquella que se basa en la competencia perfecta y el óptimo de Pareto, se está volviendo insostenible. Algo más interesante y más complicado está pasando ahí”
Paul Romer (1994). “The Origins of Endogenous Growth”
En aquel calmo mundo pre-pandémico y pre-guerra en Ucrania, precisamente en el 2018, al economista Paul Romer le fue otorgado el prestigioso Premio Nobel de Economía junto a su colega William Nordhaus. Específicamente, a Romer se les otorgo en conjunto el Nobel de Economía por sus contribuciones que permitieron formalizar e “integrar las innovaciones tecnológicas en el análisis macroeconómico a largo plazo” (Nobel Prize, 2018). Dicho de otra forma, a Paul Romer se le otorgo el Nobel por su contribución económica que nos permitió entender como formalizar matemáticamente el rol que tienen las ideas y las innovaciones tecnológicas en poder generar crecimiento económico sostenido. Quizás la contribución más importante de Romer a la ciencia económica, es que nos permitió pensar de otra forma y de forma novedosa respecto al rol clave que tienen las ideas en el proceso capitalista, y como las ideas y la innovación en los mercados son la fuente perenne que nos permite generar crecimiento económico y progreso material. Es decir, las ideas de Romer son importantes porque cambio el paradigma de entender el crecimiento endógeno al ofrecernos nuevas ideas respecto al rol clave de las ideas en el sistema capitalista.
Paul Romer estaba haciendo su disertación doctoral en Chicago en los años 80’ cuando empezó a pensar en la teoría del crecimiento y el rol de las ideas en este. Romer completó su disertación doctoral en Chicago en 1983, bajo el recién fallecido Premio Nobel Robert Lucas, titulada “Dynamic Competitive Equilibria with Externalities, Increasing Returns and Unbounded Growth” (ver aquí). Dicha disertación doctoral de 1983 serían las bases intelectuales de sus dos publicaciones clave por las cuales recibió luego el Premio Nobel: la primera publicación de 1986 “Increasing Returns and Long-Run Growth” (JPE), y luego su publicación clave y más notable de 1990 “Endogenous Technological Change” (JPE). Cuando Romer estaba comenzando a trabajar en la teoría del crecimiento económico en los 80’, la visión tradicional de los economistas estaba marcada por el modelo de Solow (1956), el cual establecía que el crecimiento económico era exógeno. Es decir, que el crecimiento de la productividad no podría verse influido por nada en el resto de la economía (factores endógenos).

Romer, construyendo desde los pasos de Solow (1956), pero sobre todo desde las ideas de rendimientos crecientes de escala y del rol de las ideas de Arrow (1962) y de Nordhaus (1969), desarrolló la teoría del crecimiento endógeno; enfatizando que el cambio tecnológico es el resultado de esfuerzos de investigadores, empresarios e inventores que responden a incentivos económicos en el mercado y en las ciencias del saber (universidades). Cualquier cosa que afecte sus esfuerzos e incentivos, como la política fiscal, los impuestos, las subvenciones, la financiación de la investigación básica y la educación, por ejemplo, puede influir potencialmente en las perspectivas a largo plazo de la economía, al alterar los incentivos para producir ideas.
En simple, la contribución esencial de Paul Romer es su clara comprensión de la economía de las ideas y cómo el descubrimiento de nuevas ideas se encuentra en el corazón del crecimiento económico y en el corazón de nuestras posibilidades de generar progreso y de escapar de las trampas Malthusianas. Su paper de 1990 “Endogenous Technological Change” (JPE), es un hito clave en la historia del pensamiento económico contemporáneo y se erige como el artículo más importante en la literatura sobre crecimiento desde el trabajo de Robert Solow reconocido también con el Nobel en 1987. Como habíamos mencionado, Romer había estado trabajando bajo Bob Lucas en el crecimiento durante alrededor de una década (1980-1990). Las ideas de su disertación doctoral de 1983 y de Romer (1986) ya abordan el tema clave de las ideas y sugieren que el conocimiento y las ideas son trascendentales para el crecimiento económico sostenido. Por supuesto, en un nivel trascendental y básico, desde los trabajos de Joseph Schumpeter en Capitalismo, Socialismo y Democracia (1942), entre otros, los economistas ya intuíamos que las revoluciones tecnológicas, las ideas y las innovaciones eran el motor de crecimiento en el sistema capitalista. Todos sabíamos que esto debía ser cierto, pero no sabíamos los mecanismos de fondo a través de los cuales esto era cierto. Pero lo que Romer nos ayudó a comprender, y lo que ninguna investigación hasta la fecha había apreciado completamente, era la naturaleza precisa del cómo esta afirmación se vuelve cierta. Como diría Romer, “en el punto más básico, una economía crece cada vez que las personas toman recursos escasos y los reorganizan de una manera que los hace más valiosos. … La historia humana nos enseña … que el crecimiento económico surge de mejores recetas [ideas], no solo de cocinar más. Las nuevas recetas [ideas] producen menos efectos secundarios desagradables y generan más valor económico por unidad de materia prima. ... el crecimiento económico surge de las ideas acerca de como utilizar los objetos escasos” (Romer, 2019).
Así las cosas, todo cambia en 1990, con el brillante ensayo de Paul Romer, “Endogenous Technological Change”. La idea clave de Romer se puede resumir de esta forma: las ideas generan posibilidades ilimitadas de progreso por la interacción de tres fenómenos: 1) la no-rivalidad de las ideas, 2) sus posibilidades de generar rendimientos crecientes de escala y 3) las ideas permiten explotar lo que se conoce como “explosión combinatoria”. Vamos a ver paso a paso estas tres ideas y sus implicancias.

Pero primero, en su nivel más elemental, tenemos que entender que las ideas son como las recetas de cocina, es decir, las ideas son recetas creadas con ingenio que nos muestran cómo crear nuevo valor económico ahí donde no existía, al re-combinar y mezclar objetos físicos y recursos materiales. Por ejemplo, si tenemos en nuestra casa 3 zanahorias, 200 gramos de harina y 3 huevos, todos por separado y sin ideas, quizás estos bienes no tengan mucho valor para nosotros. Per combinados con la idea de la receta del Carrot Cake, estos mismos bienes re-combinados pueden adquirir un valor económico mayor. No hay explotación, no hay rentismo, no hay extracción, ¡es el poder de las ideas! (sorry Marx) Podemos generar valor económico de la nada (out of thin air) gracias al poder de las ideas en re-combinar los recursos existentes. Personas brillantes como Ray Kroc (que revolucionó la producción de hamburguesas con el McDonald’s) y Henry Ford (que revolucionó la producción de automóviles), crearon valor económico adicional al re-combinar los factores de producción ya existentes de manera más eficiente con sus ideas.
1) La no-rivalidad de las ideas: primero, el rol clave que juegan las ideas en generar crecimiento sostenido y explosivo en la economía es debido a que las ideas son bienes no-rivales. En economía, hablamos de que los bienes son rivales cuando el consumo de dicho bien por parte de un consumidor impide el consumo simultáneo de dicho bien por parte de otros. Por ejemplo, un yogurt es un bien rival, ya que si yo consumo dicho yogurt las demás personas del planeta no pueden consumirlo; de hecho, la gran mayoría de los bienes tangibles y las materias primas son bienes rivales, de ahí que exista el fenómeno de la escasez y la presión de hacer un uso eficiente de los recursos escasos. Por el otro laso, se dice que algunos bienes son no-rivales cuando dichos bienes pueden ser consumidos por una persona sin prohibir el consumo simultáneo de otros. La mayoría de los ejemplos de bienes no rivales son intangibles: el teorema de Pitágoras, el idioma, las ideas, etc., son bienes que, si los consume una persona, esto no impide que otros puedan consumirlo. Por ejemplo, el hecho de que yo use la idea de la fermentación para hacer queso no impide que otros usen la misma idea simultáneamente para hacer yogurt o mantequilla, etc. ¡Esta es una de las grandes propiedades maravillosas de las ideas!
Dicho de otra forma, a diferencia de un yogurt (que es un bien rival), donde si yo lo consumo ustedes no pueden después consumirlo, las ideas se pueden consumir sin agotarlas (las ideas no se agotan con su uso). Por ejemplo, si yo uso el teorema de Pitágoras o la idea de la fermentación, mi uso no impide que ustedes lo puedan usar en otra cosa simultáneamente. Esto permite que infinitas personas al mismo tiempo puedan usar la misma idea, permitiéndonos, de cierta forma, escapar de la escasez y de los límites de los bienes materiales y de los recursos tangibles. Esta rivalidad que surge en los bienes “rivales” y tangibles, subyace a la escasez que está en el corazón de la mayor parte de la economía y da lugar a los Teoremas Fundamentales del Bienestar de la Economía. Las ideas, por el contrario, no son rivales: a medida que más y más personas usan el teorema de Pitágoras o el lenguaje de programación Java, no hay menos y menos ideas para todos. Las ideas no se agotan con el uso, y es tecnológicamente factible que cualquier número de personas use una idea simultáneamente una vez que se ha inventado.
2) La no-rivalidad de las ideas permite la posibilidad de rendimientos crecientes de escala con los recursos escasos. Para entender este punto esencial, primero tenemos que explicar brevemente que entendemos por rendimientos crecientes de escala. Vamos a tener que hace un pequeño rodeo explicativo para clarificar este concepto (si el lector ya conoce esta idea de rendimientos crecientes de escala puede saltarse la siguiente sección y seguir con las ideas de Romer más abajo).
Pequeña digresión en torno a las económicas de escala: Malthus, Ricardo y Smith
En economía existen tres tipos de rendimientos de escala: rendimientos decrecientes de escala, rendimientos constantes de escala y rendimientos crecientes de escala, como se puede ver en el gráfico 1 adjunto.

Los rendimientos decrecientes de escala (línea roja en el gráfico) significan que al agregar más factores de producción (inputs) en el sistema productivo, su producción de bienes (outputs) crece menos que proporcionalmente. Es decir, los rendimientos decrecientes señalan que si aumenta la cantidad de uno de los factores productivos (el trabajo), pero el resto se mantiene constante (el capital), la producción total aumentará de forma cada vez más lenta hasta dejar de crecer, pudiendo incluso disminuir. Por ejemplo, si tenemos una cocina pequeña y tenemos 1 chef en la cocina, este producirá 10 platos por noche, pero si añadimos 2 chefs más a la cocina pequeña, para tener así tres chefs, la producción de la cocina podrá ser de 20 platos por noche; posteriormente si agregamos 100 chefs más a la cocina la producción de platos puede ser que llegue quizás a 30 y quizás incluso la producción de platos hasta baje a 18 platos por noche. Al aumentar el número de chefs, la producción de platos no aumento de forma lineal, de hecho, hasta puede disminuir. El trabajo y la mano de obra tiende a tener rendimientos decrecientes de escala, haciendo que el trabajo, la hora hombre y el esfuerzo físico no sean la clave para generar prosperidad sostenida en el tiempo (¡sorry Marx!).
De hecho, esta idea de los rendimientos decrecientes de escala de las personas y el crecimiento poblacional es la base del pesimismo de Robert Malthus respecto a la sobrepoblación y la base de la idea de la trampa Malthusiana. Uno de los supuestos de Malthus es que hay rendimientos decrecientes de escala en la producción de bienes y alimentos, ya que hay rendimientos decrecientes en la combinación entre tierra y personas. Es decir, si duplicamos el número de personas y las ponemos a trabajar en la tierra, el aumento de producción de alimento crece en menor proporción que el aumento de personas, generando una presión demográfica por el alimento escaso. En la presencia solo de rendimientos decrecientes de escala estamos en un problema grave, ya que esto genera que al final haya muchas más personas que alimentos, produciendo una crisis demográfica y alimentaria, poniendo presión en la mortalidad, empujando a la sociedad a volver a un equilibrio más bajo de población (la sociedad no despega del estatus quo de la pobreza y la miseria con rendimientos decrecientes de escala). La previsión catastrófica del Reverendo Malthus era verdadera en el mundo medieval pre-capitalista, pero resultó evidentemente errada en el mundo capitalista post-revolución industrial, porque no se tuvieron en cuenta el desarrollo tecnológico, la destrucción creativa, ni tampoco los beneficios de las ideas que tienen rendimientos crecientes de escala (¡Malthus no alcanzo a leer a Romer!).
Los rendimientos constantes de escala (línea negra en el gráfico) significan que al agregar más factores de producción (inputs) en el sistema productivo, su producción de bienes (outputs) crece igual y en la misma proporción en la que aumentaron los factores de producción. Por ejemplo, supongamos que tenemos 1 jardín de 10m2 que produce 10 kilos de tomate, si nosotros compramos un segundo jardín de 10m2 produciríamos 20 kilos de tomate y así sucesivamente. Es decir, la producción de tomates crece en la misma proporción con la cual aumentamos el factor de producción tierra. De hecho, la tierra y el capital (como las herramientas mecánicas) generalmente tienden a tener rendimientos constantes de escala, haciendo que —matemáticamente— sean incapaces de explicar la explosión exponencial de riqueza y bienestar ocurridos en los últimos 200 años bajo el sistema capitalista (¡sorry Ricardo!).
Finalmente, tenemos aquellos esquivos rendimientos crecientes de escala (línea verde en el gráfico), que son aquellos en donde agregar más factores de producción (inputs) en el sistema productivo, su producción de bienes (outputs) aumente de forma creciente y en mayor proporción incluso de la que aumentaron los factores de producción. Los rendimientos crecientes de escala existen cuando al incrementar de 1 el input o los factores productivos, el output o producción de bienes crece más de 1, haciendo que la producción aumente más que linealmente e incluso hasta exponencialmente. El primer gran economista en darse cuenta de las grandes posibilidades de crecimiento económico y de explosión de bienestar que otorgan los rendimientos crecientes de escala fue Adam Smith. De hecho Smith, ya en la página 2 del capítulo 1 de la Riqueza de las Naciones, da el primer ejemplo que conocemos en la historia de la economía de los efectos de los rendimientos crecientes de escala gracias a la división del trabajo. Smith nos explica en su famoso ejemplo de la pin factory (fábrica de alfileres) como la división del trabajo puede llevar a mayor productividad y progreso gracias a los rendimientos crecientes de escala. De hecho, el ejemplo de la pin factory (la fabricación de alfileres) es un clásico ejemplo de rendimientos crecientes de escala a través de la división del trabajo: si 1 sola persona hace toda la producción de alfileres este podrá hacer 1 alfiler al día; pero si juntamos a 10 personas y las hacemos colaborar a través de la división del trabajo subdivididos en pequeñas tareas, esas 10 personas pueden producir 4.800 alfileres por día (Smith, p. 34-35). Esta es la razón, según Smith, por la explosión de productividad y riqueza, la capacidad de la sociedad comercial de explotar los rendimientos crecientes de escala. Esto se puede ver gráficamente en la figura 2 adjunta a la derecha.

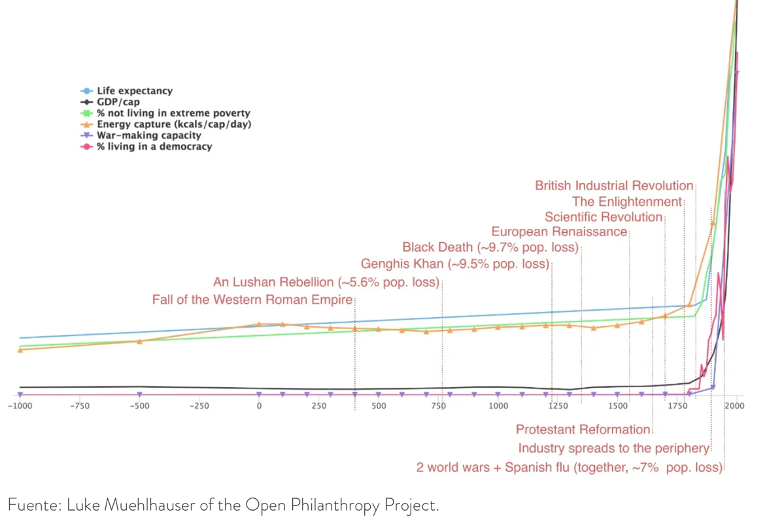
Smith, a diferencia de Malthus, Marx, Ricardo y muchos otros economistas a lo largo de estos 250 años de capitalismo, fue capaz de entender que la presencia y búsqueda constante de rendimientos crecientes de escala, es lo que puede ayudarnos a escapar de las trampas Malthusianas y escapar de la presión que nos impone la escasez de los recursos productivos y la presión demográfica. La constante búsqueda de rendimientos crecientes de escala en el sistema capitalista es lo que subyace finalmente al motor de prosperidad y de crecimiento económico exponencial nunca antes visto en la historia de la humanidad, denominado hoy como “el gran escape” o “el palo de hockey de la prosperidad humana”, como se pude ver el gráfico 3 abajo.
Esta idea brillante de las grandes posibilidades de progreso a través de los rendimientos crecientes de escala que nace con Adam Smith, lamentablemente cayó en el olvido en la historia del pensamiento económico por más de 150 años hasta que el economista Allyn A. Young la rescatara en 1928 del olvido con su famoso paper “Increasing Returns and Economic Progress”. Después de Young en 1928, brillantes economistas Premios Nobel como Buchanan (Buchanan and Yoon, 2000; Buchanan and Yoon, 1994) y Arrow (1962) rescataron esta idea hasta llegar a Paul Romer y sus artículos clave de 1987 “Growth Based on Increasing Returns Due to Specialization” y de 1986 “Increasing Returns, Specialization, and External Economies: Growth as Described by Allyn Young”. Para ver una reseña interesante de la historia intelectual de la idea de rendimientos crecientes de escala consultar: Cómbita Mora (2012) y Guillermo Peon (2003). Es el momento entonces de volver a Romer y al poder de las ideas.
Volviendo a Romer y las ideas con rendimientos crecientes de escala
Volviendo a Romer entonces, ¿cómo explica la no-rivalidad de las ideas el crecimiento económico exponencial visto en los últimos 200 años? La clave de la magia es que la no-rivalidad de las ideas da lugar a rendimientos crecientes de escala en el sistema económico. El argumento estándar de la replicación en la producción de bienes (standard replication argument) es una justificación fundamental para obtener los rendimientos constantes a escala en la producción. Si deseamos duplicar la producción de computadoras de una fábrica, una forma factible de hacerlo es construir una segunda fábrica similar al otro lado de la calle y llenarla con trabajadores, materiales, etc., de forma equivalentes. Es decir, replicamos la fábrica exactamente para producir el doble de computadores. Esto significa que la producción con bienes rivales y capital es, al menos como punto de referencia útil, un proceso de rendimientos constantes de escala. En otras palabras, el argumento de replicación señala que la forma estándar de justificar rendimientos constantes a escala en una función de producción: si deseamos duplicar la producción de teléfonos móviles, podemos replicar exactamente la configuración de producción existente. Es decir, construimos una fábrica idéntica, contratamos un número y tipo de trabajadores idénticos y utilizamos una colección idéntica de insumos. Esto debería duplicar la producción, proporcionando una justificación para rendimientos constantes. Pero las ideas nos permiten escapar de los límites de los rendimientos constantes de escala del capital, veamos esto con un ejemplo intuitivo.
Por ejemplo, supongamos que tenemos 1 pedazo de tierra que produce 10 unidades de alimento (1T = 10A), la única posibilidad de producir 20 u. de alimentos (asumiendo que no hay tecnología) es teniendo 2 pedazos de tierra que produzcan 10 unidades c/u (1T + 1T = 20A). El capital y la tierra tiene rendimientos constantes de escala. Ahora bien, imaginemos la llegada de las ideas, y que podemos crear una idea que se llama "fertilizante", que nos permite ser más productivos con la tierra, llevando la producción desde 10 u. de alimento por tierra a 20 unidades por tierra (1T + 1F = 20A); ahora entonces, después de la creación de la idea, los dos pedazos de tierra pueden usar simultáneamente la idea de fertilizante (ya que es no-rival y el consumo de uno no impide el consumo del otro de la idea), expandiendo así la producción a 40 unidades (2T + 1F = 40A), permitiendo generar rendimientos crecientes de escala a pesar de que la tierra tiene rendimientos constantes de escala (ambas tierras juntas antes de la idea producían solo 20 u.).
En el mundo de la economía de las cosas entonces, la única forma de incrementar más la producción es aumentando el número de recursos escasos o el espacio de tierra que tenemos, lo que lleva al conflicto por dichos recursos (la única forma de pasar a 20 unidades es tener 2 tierras); por el otro lado, en la economía de las ideas, podemos bypasear este problema al utilizar 1 misma idea compartida para más que duplicar el producto sin necesidad de pelear por los recursos escasos (la introducción de 1 idea nos lleva a 40 unidades con la misma cantidad de bienes escasos originales). Las ideas y su no-rivalidad entonces más que compensan el problema que nos impone la escases de los recursos.

La maravilla subyacente es que la idea, al ser no-rival, nos permite utilizarla a destajo, copiarla y complementar los bienes escasos como el capital y la tierra que solos tienen rendimientos constantes de escala; pero ahora combinados con las ideas (como el fertilizante) ¡juntos adquieren rendimientos crecientes de escala! (en el ejemplo 2 tierras sin ideas producen 20 alimentos, 2 tierras con 1 idea producen 40 alimentos). Dicho de otra forma, dado que hay rendimientos constantes de escala en los insumos rivales (la fábrica, la tierra, los trabajadores y los materiales), podemos escapar a esos límites gracias a las ideas y obtener rendimientos crecientes de escala para los mismos insumos y bienes rivales, pero ahora mezclados con ideas tomados en conjunto. Este efecto multiplicador de las ideas y de los rendimientos crecientes de escala que pueden generar, son enormes y subyacen a la explosión de bienestar que ha ocurrido en los últimos 200 años desde el nacimiento del capitalismo.
En el ejemplo de la tierra, si se duplican los insumos rivales y además se mejoran la calidad y/o cantidad de las ideas, la producción total de alimento aumentará más del doble, produciendo una explosión de producción, productividad y crecimiento económico. Una vez que podemos obtener constantemente rendimientos crecientes de escala, gracias a la posibilidad de crear y mezclar ideas, las posibilidades de progreso y de crecimiento económico son ilimitadas. Dado que hay rendimientos constantes o decrecientes a escala en los insumos rivales (la fábrica, los trabajadores y los materiales) estamos limitados en generar progreso y las trampas Malthusianas vuelven a asecharnos; pero la magia esta que ahora estos mismos insumos rivales, pueden ser ahora mezclados con las ideas, permitiendo obtener rendimientos crecientes de escala para aquellos mismos insumos rivales e ideas tomados en conjunto: si se duplican los insumos rivales y además la calidad o cantidad de las ideas, entonces podemos más que duplicar la producción total, ¡las posibilidades de progreso resultan entonces casi ilimitadas mientras sepamos crear siempre más y mejores ideas! El optimismo de progreso de Smith pareciera tener razón y el pesimismo de Malthus pareciera estar infundado, mientras sepamos crear y difundir buenas ideas. Una vez que obtenemos rendimientos crecientes, matemáticamente, el crecimiento económico exponencial sigue naturalmente. La producción por persona depende entonces del acervo total de conocimiento e ideas; el stock total de ideas no necesita ser dividido y repartido entre todas las personas en la economía, lo que hace la gran diferencia.
Comparemos esto con el rol que juega el capital físico y los medios de producción en el modelo de crecimiento de Solow (1956). Por ejemplo, si agregamos 1 motosierra física al proceso de producción de un leñador, esto hace que solo 1 trabajador pueda ser más productivo en cortar madera y nadie más. El capital entonces tiene pocas capacidades de tener un gran impacto en el crecimiento económico a lo largo de todo el sistema (i.e., tiene pocos spillover effects). Pero si agregamos una nueva idea en la economía, como por ejemplo el código de computadora para la primera hoja de cálculo de Excel o el procesador de textos o incluso el Internet, estas ideas pueden hacer que cualquier número infinito de trabajadores sea más productivo al utilizar esa misma idea de forma simultánea (la idea de la hoja de cálculo es no-rival, mientras que la motosierra tangible lo es). De esta forma las ideas no afectan a 1 sola persona como el capital, sino que pueden impactar a una cantidad infinita de personas simultáneamente aumentando la productividad, no solo de 1 persona sino que de innumerables personas al mismo tiempo (i.e., tienen enormes efectos de spillover a lo largo de la economía). Con la no rivalidad, el crecimiento de los ingresos por persona está ligado al crecimiento del stock total de ideas (un agregado), no al crecimiento de las ideas por persona.
3) Explosión combinatoria: la tercera y última propiedad clave de las ideas es lo que se conoce hoy como “explosión combinatoria”. Es decir, las explosiones combinatorias ocurren en algunos problemas numéricos cuando la complejidad aumenta rápidamente, ya que es causada por el aumento del número de posibles combinaciones de las entradas (inputs). Esta explosión de complejidad puede hacer que algunos problemas matemáticos sean intratables, pero para las ideas (que son no-rivales) esto es una bendición. La idea de la explosión combinatoria es similar a la propiedad de la capitalización compuesta (compounding): las posibilidades simplemente no se suman de forma lineal; si no que se multiplican.

En palabras de Romer: “para tener una idea de cuánto margen hay para más descubrimientos de este tipo, lo podemos calcular de la siguiente manera. La tabla periódica contiene alrededor de 100 tipos diferentes de átomos. Si una receta es simplemente una indicación de si un elemento está incluido o no, habrá recetas de 100 x 99 como la del bronce o acero, que involucran solo dos elementos combinados. Para recetas que pueden tener cuatro elementos juntos, hay 100 x 99 x 98 x 97 recetas, que son más de 94 millones de opciones. Con hasta 5 elementos combinados, más de 9 mil millones. Los matemáticos llaman a este aumento en el número de combinaciones ‘explosión combinatoria’. Una vez que llegas a combinar 10 elementos, hay más recetas que segundos desde que el big bang creó el universo’” (Romer, 2019). Todo esto se puede ver de forma visual en la tabla adjunta al lado derecho. Imaginen todas las cosas asombrosas que se pueden hacer y crear con las distintas mezclas de átomos que simplemente nunca se han probado hasta ahora (NotCo nos da algunos indicios de lo que se puede hacer al explotar esta idea con machine learning).
Mercados, ciudades, universidades e ideas
A diferencia del modelo de Solow, en el modelo de Romer (1990), más investigadores producen más ideas que pueden ser copiadas, revisadas y mejoradas por un gran número de personas, lo que hace que todos estén mejor debido a la no-rivalidad de estas y a que ayudan a crear rendimientos crecientes de escala a mezclarse con el capital. A lo largo de la historia, gracias a la ciencia, la academia, los mercados y la escritura, el mundo se ha caracterizado por un crecimiento sustancial tanto en el stock total de ideas como en el número de personas que las crean. Según la teoría de Romer, esto es lo que sustenta el crecimiento exponencial a largo plazo. Como diría Paul Romer: “Una de las ideas más importantes es esta noción de conexión. Las personas se vuelven increíblemente productivas si pueden hacer la conexión correcta, trabajar juntas en equipos, conectarse en las cadenas productivas de las empresas [a través de los mercados] y producir así colectivamente cosas que ninguno de ellos puede hacer por sí solo. Entonces, ¿qué se necesita para estimular la conexión entre las personas?” (Paul Romer, 2018). Cuando reconocemos el rol clave que tienen la creación, difusión y mejora de las ideas y el cómo conectar a las personas para generar rendimientos crecientes de escala, entonces comprendemos finalmente el rol fundamental que tienen hoy las ciudades, las universidades y los mercados como elementos o trampolines que incentivan la creación, el testeo y la copia (o mezcla) de ideas.
En palabras de Romer: “Cada generación ha percibido los límites al crecimiento que plantearían los recursos finitos y los efectos secundarios indeseables si no se descubrieran nuevas recetas o ideas. Y cada generación ha subestimado el potencial para encontrar nuevas recetas e ideas. Siempre fallamos en comprender cuántas ideas quedan. La dificultad es la misma que tenemos para entender el interés compuesto: las posibilidades de las ideas no solo se suman, sino que se multiplican [combinatorial explotion] … Una de las mayores meta-ideas de la vida moderna es permitir que las personas vivan juntas en densas aglomeraciones urbanas. Una segunda es permitir que las fuerzas del mercado guíen la mayoría de las decisiones detalladas que toman estas personas sobre con quién interactúan entre sí. Juntos, la ciudad y el mercado permiten que grandes grupos de personas cooperen descubriendo nuevas ideas, compartiéndolas y aprendiendo unos de otros” (Romer, 2019). De hecho, el crecimiento exponencial de China en las últimas cuatro décadas es debido gracias a que China ha abrazado estas dos grandes meta-ideas: las ciudades hiperconectadas y los mercados.
En explorar la estructura profunda del rol de las ideas en el crecimiento económico a través de las ciudades y los mercados, Paul Romer hace eco tanto de las ideas de “destrucción creativa” de Schumpeter, como también de lo que el Premio Nobel de Economía F.A. Hayek ya intuía décadas atrás respecto al verdadero rol del mercado y la competencia en este, que actúan como verdaderos “procesos de descubrimiento” de nuevas ideas a traves de la competencia descentralizada en el mercado (Hayek, 1946; Hayek, 1968). En el mercado entonces, es el lugar en donde ocurre el testeo masivo y descentralizado de ideas en donde estamos constantemente introduciendo nuevas ideas, mezclando ideas antiguas con ideas nuevas y estamos copiando y diseminando ideas que funcionan a lo largo de la economía (Bento, 2014). Los mercados son finalmente un mecanismo de interacción y de cooperación social que fomenta con incentivos económicos y con señales de ganancia/perdida la producción, combinación y transmisión de ideas de forma permanente en la sociedad. Con todo, el mercado y el sistema competitivo de empresas en el capitalismo (con derechos de propiedad en las innovaciones) son el complemento clave para que los avances científicos puedan aplicarse, escalarse, testearse y así generar mayor prosperidad y más crecimiento económico. Como diría Romer, la economía de mercado es “esta enorme máquina de descubrimiento de innovación” (Romer, 2018).
El sistema de mercado y la competencia entre empresas privadas ayuda a promover: 1) Incentivos económicos para innovar y para divulgar tus ideas: como bien estableciera Schumpeter, los mercados y la propiedad privada generan incentivos económicos muy fuertes para que las personas traten de crear ideas nuevas y de crear avances científicos que sean útiles para las personas. El hecho de que hay avances científicos que puedan tener valor económico y generar ganancias es un incentivo fuerte para tratar de crear nuevas ideas y utilizar la ciencia y así generar un valor práctico. 2) Proceso de ensayo/error: el mercado permite un proceso descentralizado de ensayo error con recursos personales (con skin-in-the-game) y no con los recursos de todos, en donde las empresas pueden testear ideas y probarlas en el mercado para ver si la gente las valora y para ver si poseen utilidad pública. 3) Los mercados permiten conectar y concatenar rápidamente ideas: como estableciera Hayek (2013), los mercados son redes de colaboración dinámicos que permiten una gran comunicación y colaboración entre personas, aumentando la posibilidad de que conectemos, mezclemos, y concatenemos unas ideas con otras, aumentando el efecto de knowledge spillover y exacerbando el efecto de “explosión combinatoria”. En palabras de Romer (2018): “Hay una cultura de innovación en evolución junto a nuevas empresas en el mercado (startups), que es realmente donde tienen lugar la mayoría de las aplicaciones prácticas de las ideas. Entonces, el sistema de la ciencia está interactuando constantemente con el mercado. Estamos constantemente modificando nuestras instituciones científicas y a su vez trabajando para que sea más fácil para las empresas abrir y comenzar, para que después las nuevas ideas puedan probarse con los consumidores”.
En síntesis, la clave para el crecimiento bajo el capitalismo es que el bienestar y el progreso tienen que ver con el uso práctico de las ideas, cómo estas se pueden copiar, implementar, modificar, combinar, etc., para producir constantemente más nuevas ideas y así explotar rendimientos crecientes de escala. Esto es posible gracias al hecho de que las ideas son 1) no-rivales y 2) crean efectos indirectos (externalidades positivas en la forma de knowledgespillovers). Las ideas crean efectos indirectos positivos casi infinitos a través de un ‘loop positivo’ virtuoso: es decir, las ideas se pueden copiar, mezclar y agrupar (o mezclar) siempre de manera nueva e inesperada, creando luego más y nuevas ideas, que luego se agregan al stock original para luego volver a combinarse con viejas ideas, para luego producir aún más ideas en un ciclo interminable de posibilidades combinatorias. Esto crea la posibilidad de una explosión exponencial de crecimiento y riqueza. No hay límite para la producción de ideas y su mezcla, ya que las posibles combinaciones entre las ideas y las cosas materiales es casi infinito, produciendo posibilidades ilimitadas para generar prosperidad.
Por ejemplo, imaginen que hay solo 100 ideas en el mundo. Si queremos combinar 3 de estas 100 ideas, las posibilidades combinatorias son 100 x 99 x 98 = 970,200 nuevas combinaciones posibles. Imaginen que de esas 970,200 nuevas combinaciones salgan 3 ideas buenas de estas mezclas, haciendo que el stock de ideas ahora pase a 103. Las posibilidades combinatorias de mezclar 3 ideas del stock nuevo son 103 x 102 x 101 = 1.061.106 y así sucesivamente. Por lo demás, estos números explotan en magnitud si en vez de mezclar 3 ideas, decidimos mezclar 5 ideas al mismo tiempo, ya que las posibilidades combinatorias serían 103 x 102 x 101 x 100 x 99 = 10.504.949.400 y así sucesivamente mezclando la no-rivalidad de las ideas con su explosión combinatoria. En otras palabras, la propiedad de la no-rivalidad interactúa con la propiedad de la ‘explosión combinatoria’, haciendo posible un incremento exponencial sin límites de descubrir nuevas ideas para usar los recursos escasos de mejor manera. De hecho, una de las paradojas del modelo de Romer es que si nos tomamos en serio que las ideas son no-rivales y la idea de ‘explosión combinatoria’, entonces el crecimiento económico ilimitado y sin fin es posible incluso en un mundo rodeado por la escasez y por recursos finitos. Esto es porque las propiedades de las ideas más que compensan (offset) las propiedades rivales de los bienes escasos.
Al igual que Joseph Schumpeter en Capitalismo, Socialismo y Democracia (capítulos 7 y 8), Romer enfatiza que es probable que sean importantes tanto la competencia imperfecta (posiciones dominantes transitorias) como las externalidades positivas del conocimiento para el descubrimiento de nuevas ideas (knowledge spillovers). La competencia monopolística, las posiciones transitorias dominantes y los derechos de propiedad asociados a las innovaciones y a las ideas, proporciona las ganancias económicas que actúan como incentivos para que los empresarios y los científicos innoven. Y los inventores e investigadores posteriores se benefician además del copiar y mezclar libremente las ideas existentes de los que vinieron antes.

Finalmente, la posibilidad de seguir expandiendo el progreso económico para todos y de escapar de las trampas Malthusianas que llevan a la miseria, descansa en nuestra capacidad de promover y seguir explotando los rendimientos crecientes de escala que existen a través del comercio internacional, la especialización, la división pacífica del trabajo, el copiar y mejorar las ideas científicas, y de promover el espíritu empresarial de la destrucción creativa que permite impulsar las innovaciones tecnológicas en los mercados (Aghion, et al. 2020). Nuestras ideas hoy sobre el crecimiento económico y las posibilidades (casi) ilimitadas del progreso material (gracias a las ideas dentro del sistema capitalista), han sido monumentalmente influenciadas por las contribuciones clave de Paul Romer, y todos los economistas hoy preocupados del progreso material y de cómo promover el crecimiento entendemos la importancia de explotar los rendimientos crecientes de escala ya que estamos parados sobre los hombros de gigantes como Smith, Arrow y Romer.





Comments